7 1 Odds
Save / Share This Bet Slip
What is an each way bet? - Learn about the each way bet and all its possible outcomes. This bet can generate a return even when your selection doesn't win outright. Discover how the returns are calculated and follow the detailed examples.
Double bet calculator - For an each way wager with 2 selections, use this calculator. Please be sure to manually select the Each Way option from the dropdown box. Both selections must at least place to gain a return.
When you select your 7 th number, you have 44 numbers to choose from, and.a 1 in 44 chance of picking the right one. (Mathematically, 1 in 44 is represented by the numerical fraction 1 / 44 or 0.022727.) In order to win, you have to pick the first number right AND the second number right AND the third number right, etc. Cleveland Cavaliers: 7/1 It can quickly be determined that the Golden State Warriors are the favorites while the odds on Houston and Cleveland winning are longer. That is, one wins only $10 against.
Treble bet calculator - Combine 3 selections into an each way treble and calculate the returns with this calculator. Just choose the option from the drop down menu and enter your details. Note that all selections must finish in a placing position to achieve a return.
Accumulator bet calculator - Supports up to 20 selections in an each way accumulator. Choose your options and enter the odds for the returns to be calculated. Supports rule 4 deductions, dead heats, non runners, fold betting and more.
71 Olds 88
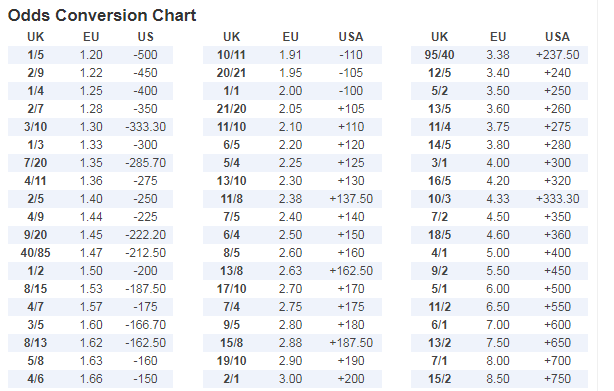
Each Way Bet Calculator FAQ
An Each Way bet is essentially split into 2 bets. The first part of the bet is a WIN bet on your selection, and the second is that they will PLACE, the place bet will vary per race or event, but it will generally be to finish in the top 4 or 5.
When you place an Each Way bet your stake is doubled; so a £5 Each Way bet would require a £10 stake. £5 will go on the win portion and £5 on the place portion.
The place portion of the bet will be represented using a fraction of the winning odds. So for instance, if the each way fraction is 1/5 and the winning odds are 10/1 and you place a £5 each way bet, then your win portion has potential returns of £55 (£50 + £5) and the place portion potential returns of £15 (£10 + £5). If your selection wins you will receive both these returns if they place then you will only receive the second returns for that portion of the bet.
7-1 Odds Payout
The main advantage of an Each Way bet is that it increases your chance of a win. If the odds are long already then the potential returns if your selection places may still be attractive.
On the downside Each Way bets require a greater initial stake as your stake is essentially doubled and if your selection already has low odds then the returns may be significantly less attractive once you discount the win portion of your stake.
Calculator Use
Convert stated odds to a decimal value of probability and a percentage value of winning and losing. This calculator will convert 'odds for winning' an event or 'odds against winning' an event into percentage chances of both winning and losing.
Be careful if you are using sports teams odds or betting odds. If you see that the Patriots super bowl odds are 9/2, that is most likely 'odds against' and should be entered in the calculator with 'Odds are: against winning.'
When playing a lottery or other games of chance be sure you understand the odds or probability that is reported by the game organizer. A 1 in 500 chance of winning, or probability of winning, is entered into this calculator as '1 to 500 Odds are for winning'. You may also see odds reported simply as chance of winning as 500:1. This most likely means '500 to 1 Odds are against winning' which is exactly the same as '1 to 500 Odds are for winning.'
Probability Formulas:
This calculator will convert 'odds of winning' for an event into a probability percentage chance of success.
Odds, are given as (chances for success) : (chances against success) or vice versa.
If odds are stated as an A to B chance of winning then the probability of winning is given as PW = A / (A + B) while the probability of losing is given as PL = B / (A + B).
For example, you win a game if you pull an ace out of a full deck of 52 cards. Pulling any other card you lose. The chance of winning is 4 out of 52, while the chance against winning is 48 out of 52 (52-4=48). Entering A=4 and B=48 into the calculator as 4:48 odds are for winning you get
For 4 to 48 odds for winning;
Probability of:
Winning = (0.0769) or 7.6923%
Losing = (0.9231) or 92.3077%
'Odds for' winning: 1:12 (reduced from 4:48)
'Odds against' winning: 12:1 (reduced from 48:4)